Coding out Self Balancing Tree data structures
Over the past month, I decided to go down the rabbit hole of exploring an example of a self balancing tree data structure. I generally don’t need to handle data structures on a day to day basis - I mostly deal with integration of tools as well as deployment of tools into a Kubernetes cluster. However, even if I don’t deal with that side of things, I do find that some of the thought process behind the data structures and algorithms are pretty interesting. (I’m still kind of waiting for a moment where I can actually utilize it in my work for real in a way)
A self balancing binary tree is kind of a extension of the usual binary tree. In a binary tree, in order to make it useful, we would use it to arrange incoming data - thereby, we can immediately print the values in a sorted manner. However, the binary tree as it is comes with its own set of weakness; which can be demonstrated in the following example.
Let’s say we have a binary tree where data that is less that root is inserted to the left of the root and data that is more than the right is sorted to the right. If we are to insert data into tree in the following order: 20, 30, 10; we will get the following tree.
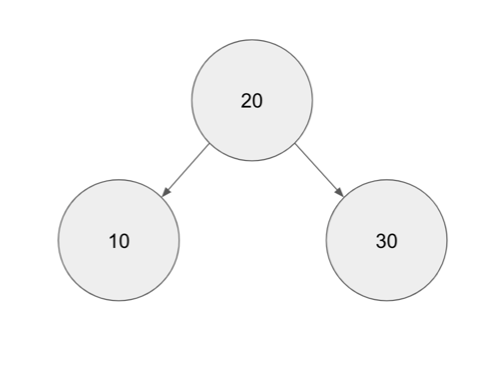
If we attempt to do inserts or searching whether an element exists in the tree, we would ideal hit a time complexity of O(log(n))
However, if the order of the input changed to 10, 20 and then 30, the tree (following the above logic) would result in the following structure.
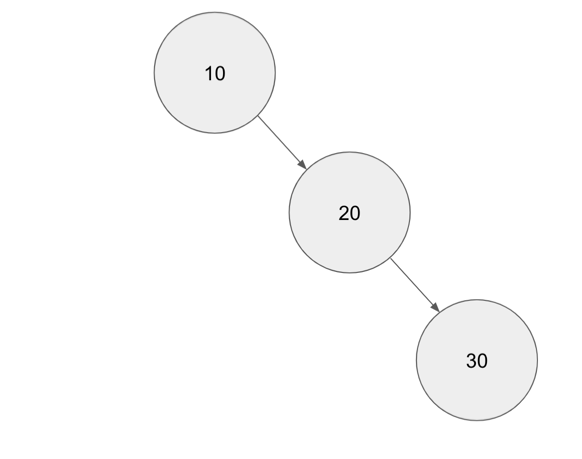
In this case, assuming a worst case scenario, potentially, our binary tree would almost become like a Singly Linked list if the item being fed to the tree is a ordered list. Potential time complexity in this scenario is O(n).
How can we improve this? We can do so by adding the capability for the tree to automatically self balanced itself the moment it detects that it is imbalanced in any way. One example of a self balancing binary tree is AVL tree - named after its inventors (Adelson-Velsky and Landis). The following video explains the concepts way better as compared to what that would be covered in this blog post. This blog post would focus more on an attempt of an implementation of the AVL tree structure.
The first part is to define the “nodes” that would comprise of the tree:
type Node struct {
Value int
Left *Node
Right *Node
}
The next parts would definitely be create 2 types of printing functions. One is to test the tree’s capability to ensure that no matter, its “Inorder” printing of the tree would always be printing a sorted list. (Inorder printing prints from left most nodes first before printing the root nodes and finally, the right nodes)
func InorderPrint(root *Node) {
if root == nil {
return
}
if root.Left != nil {
InorderPrint(root.Left)
}
fmt.Println(root.Value)
if root.Right != nil {
InorderPrint(root.Right)
}
}
The other printing function that we would need is more of a level based printing function that would serve more for debugging purposes (to see the number of levels in the tree as well as to see the data that is printed on per level basis)
func PrintLevel(root *Node, currentLevel, level int) {
if root == nil {
return
}
if currentLevel == level {
fmt.Println(root.Value)
}
PrintLevel(root.Left, currentLevel+1, level)
PrintLevel(root.Right, currentLevel+1, level)
}
Naturally, we would also need to have a function to create a function that prints out the maximum depth of the tree (also for debugging as well as to help us iterate the PrintLevel function)
func MaxDepth(root *Node) int {
if root == nil {
return 0
}
numL := MaxDepth(root.Left) + 1
numR := MaxDepth(root.Right) + 1
if numL >= numR {
return numL
}
return numR
}
Once, we have all the above functions, we can finally move to the most critical bit, which is the Insert function. There are a few things that we would need to handle (do make sure to watch the youtube video above since most of this algo is implemented here is based on that)
- Checking for imbalance of Left Hand side of tree and Right Hand side of tree
- LL rotation of tree nodes
- RR rotation of tree nodes
- LR rotation of tree nodes (complex scenario - imagine data nodes coming in is 30, 10 and lastly 20 - the tree has to be manipulated in a weird way to ensure balance)
- RL rotation of tree nodes (complex scenario - imagine data nodes coming in is 30, 10 and lastly 20 - the tree has to be manipulated in a weird way to ensure balance)
The algo implemented attempts to cover all of the above (there could be bugs so make sure take a grain of salt while reading the codebase)
func Insert(root *Node, newNode *Node) *Node {
if root == nil {
return newNode
}
if newNode.Value <= root.Value {
root.Left = Insert(root.Left, newNode)
} else {
root.Right = Insert(root.Right, newNode)
}
LH := MaxDepth(root.Left)
RH := MaxDepth(root.Right)
LHBalance := 0
RHBalance := 0
if root.Left != nil {
LHBalance = MaxDepth(root.Left.Left) - MaxDepth(root.Left.Right)
}
if root.Right != nil {
RHBalance = MaxDepth(root.Right.Left) - MaxDepth(root.Right.Right)
}
// Left hand side too heavy
if (LH-RH) >= 2 && LHBalance >= 0 {
newRoot := root.Left
root.Left = newRoot.Right
newRoot.Right = root
return newRoot
}
// Right hand side too heavy
if (LH-RH) <= -2 && RHBalance <= 0 {
newRoot := root.Right
root.Right = newRoot.Left
newRoot.Left = root
return newRoot
}
// Double rotation cases
if (LH-RH) >= 2 && LHBalance < 0 {
newRoot := root.Left.Right
root.Left.Right = nil
newRoot.Left = root.Left
root.Left = newRoot.Right
newRoot.Right = root
return newRoot
}
// Double rotation cases
if (LH-RH) <= -2 && RHBalance > 0 {
newRoot := root.Right.Left
root.Right.Left = nil
newRoot.Right = root.Right
root.Right = newRoot.Left
newRoot.Left = root
return newRoot
}
return root
}
With that, now we have all the required basic functionality that we would need in order to test the automatic self balanced binary tree. We can do so in the following Golang codebase:
// This package is meant for building a self balancing BST (AVL)
package main
import "fmt"
type Node struct {
Value int
Left *Node
Right *Node
}
func InorderPrint(root *Node) {
if root == nil {
return
}
if root.Left != nil {
InorderPrint(root.Left)
}
fmt.Println(root.Value)
if root.Right != nil {
InorderPrint(root.Right)
}
}
func MaxDepth(root *Node) int {
if root == nil {
return 0
}
numL := MaxDepth(root.Left) + 1
numR := MaxDepth(root.Right) + 1
if numL >= numR {
return numL
}
return numR
}
func PrintLevel(root *Node, currentLevel, level int) {
if root == nil {
return
}
if currentLevel == level {
fmt.Println(root.Value)
}
PrintLevel(root.Left, currentLevel+1, level)
PrintLevel(root.Right, currentLevel+1, level)
}
func Insert(root *Node, newNode *Node) *Node {
if root == nil {
return newNode
}
if newNode.Value <= root.Value {
root.Left = Insert(root.Left, newNode)
} else {
root.Right = Insert(root.Right, newNode)
}
LH := MaxDepth(root.Left)
RH := MaxDepth(root.Right)
LHBalance := 0
RHBalance := 0
if root.Left != nil {
LHBalance = MaxDepth(root.Left.Left) - MaxDepth(root.Left.Right)
}
if root.Right != nil {
RHBalance = MaxDepth(root.Right.Left) - MaxDepth(root.Right.Right)
}
// Left hand side too heavy
if (LH-RH) >= 2 && LHBalance >= 0 {
newRoot := root.Left
root.Left = newRoot.Right
newRoot.Right = root
return newRoot
}
// Right hand side too heavy
if (LH-RH) <= -2 && RHBalance <= 0 {
newRoot := root.Right
root.Right = newRoot.Left
newRoot.Left = root
return newRoot
}
// Double rotation cases
if (LH-RH) >= 2 && LHBalance < 0 {
newRoot := root.Left.Right
root.Left.Right = nil
newRoot.Left = root.Left
root.Left = newRoot.Right
newRoot.Right = root
return newRoot
}
// Double rotation cases
if (LH-RH) <= -2 && RHBalance > 0 {
newRoot := root.Right.Left
root.Right.Left = nil
newRoot.Right = root.Right
root.Right = newRoot.Left
newRoot.Left = root
return newRoot
}
return root
}
func main() {
aa := Node{Value: 30}
bb := Node{Value: 20}
cc := Node{Value: 10}
dd := Node{Value: 15}
ee := Node{Value: 17}
ff := Node{Value: 18}
zz := Insert(nil, &aa)
zz = Insert(zz, &cc)
zz = Insert(zz, &bb)
zz = Insert(zz, &dd)
for i := 1; i <= MaxDepth(zz); i++ {
fmt.Printf("Print level %v\n", i)
PrintLevel(zz, 1, i)
}
fmt.Println("Done")
zz = Insert(zz, &ee)
zz = Insert(zz, &ff)
InorderPrint(zz)
fmt.Println(MaxDepth(zz))
for i := 1; i <= MaxDepth(zz); i++ {
fmt.Printf("Print level %v\n", i)
PrintLevel(zz, 1, i)
}
}
It’s a pretty interesting exercise and for sure, it can be extended way more in varied directions in order to understand the algorithm/data structure further. It’s still sad that I haven’t exactly found any exact place for when to actually use it so this is in the hopes for coming across such a situation in my day to day work.